Analysis and Synthesis of Digital Dyadic Sequences

Abdalla G. M. Ahmed, Mikhail Skopenkov, Markus Hadwiger and Peter Wonka

ACM Transactions on Graphics, Vol.42, No.6 (Proceedings ACM SIGGRAPH Asia 2023), pp. 218:1-218:17 , 2023

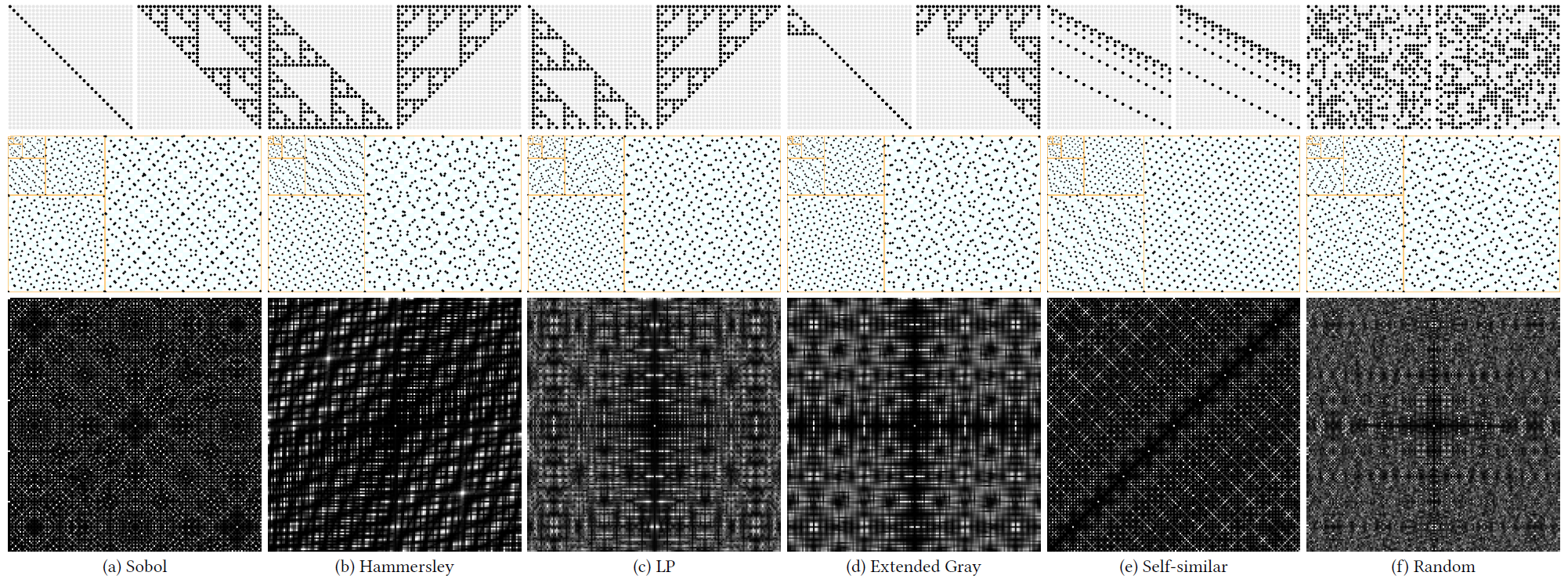
We explore the space of matrix-generated (0, m, 2)-nets and (0, 2)-sequences in base 2, also known as digital dyadic nets and sequences. In computer graphics, they are arguably leading the competition for use in rendering. We provide a complete characterization of the design space and count the possible number of constructions with and without considering possible reorderings of the point set. Based on this analysis, we then show that every digital dyadic net can be reordered into a sequence, together with a corresponding algorithm. Finally, we present a novel family of self-similar digital dyadic sequences, to be named xi-sequences, that spans a subspace with fewer degrees of freedom. Those xi-sequences are extremely efficient to sample and compute, and we demonstrate their advantages over the classic Sobol (0, 2)-sequence.

@article{Ahmed2023DigitalDyadicSequences,
  title = {Analysis and Synthesis of Digital Dyadic Sequences},
  author = {Ahmed, Abdalla G. M. and Skopenkov, Mikhail and Hadwiger, Markus and Wonka, Peter},
  journal = {ACM Transactions on Graphics (Proceedings ACM SIGGRAPH Asia 2023)},
  year = {2023},
  volume = {42},
  number = {6},
  pages = {218:1--218:17}
}